Physics-Informed Neural Networks (PINNs) embody a transformative approach in scientific machine learning (SciML), enabling a seamless fusion of observational data with the intrinsic structure of physical laws. This blog delves into what makes PINNs a pivotal advancement in the scientific method, underlining their potential to redefine how we model, analyse, and understand complex physical phenomena.

PINNs in MATLAB

The Evolution of Scientific Inquiry with PINNs

Machine learning has augmented the scientific method, shifting the paradigm from a theory-experiment cycle to a data-centric approach. However, the reliance solely on data-driven methodologies often leads to models that may need more generalisability or to encapsulate the underlying physical principles governing the phenomena in question. Herein lies the significance of PINNs – they learn from data and imbibe the foundational equations of physics into their learning process, ensuring that the models adhere to the established laws of nature.

A physics-informed neural network learning to model a harmonic oscillator (Source)

The journey to utilise the full potential of PINNs has its challenges. Training inefficiencies and the pitfalls of suboptimal configurations, often stemming from a limited understanding of deep learning intricacies, can significantly impede the effectiveness of these networks.

To navigate these hurdles and unlock the robust capabilities of PINNs, recent advancements have emphasised the importance of adopting best practices in their training and implementation. This blog is offering insights into how they enhance training efficiency and bolster the accuracy of PINNs.

As we delve deeper into the synthesis of machine learning and physical laws, PINNs emerge as a beacon of innovation, promising to redefine our approach to problem-solving in domains where data and physics converge. By embracing the best practices and insights gleaned from rigorous studies, the field stands on the cusp of unlocking new horizons, where the predictive prowess of deep learning is seamlessly married with the unassailable truths of physical science.

Understanding Physics-Informed Neural Networks (PINNs)

At their core, PINNs represent a sophisticated blend of deep learning and physics. They empower computers to not only learn from data but also to adhere to the "rules of the game" set by physical laws. This capability enables machines to tackle complex problems across various domains, from science to engineering, with an enhanced level of understanding and precision.

The Essence of PINNs

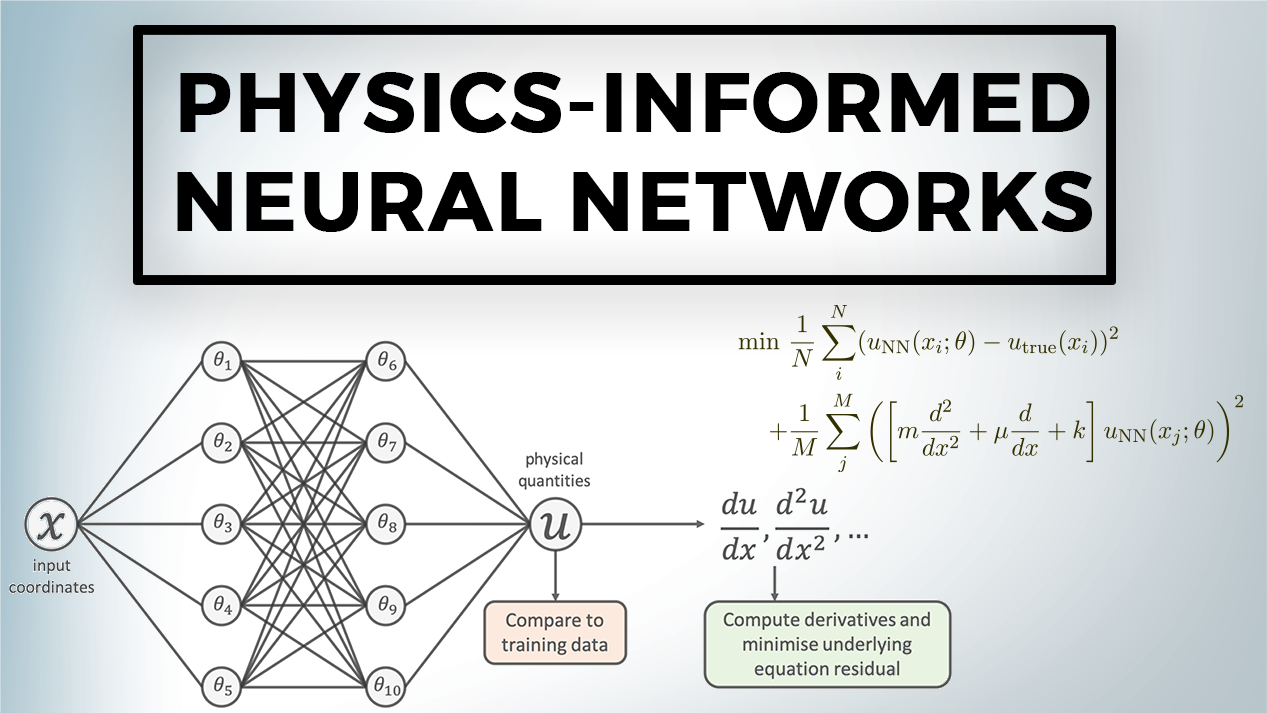
A physics-informed neural network (PINN) is a specialised type of neural network designed to integrate and adhere to the fundamental laws of physics directly within its learning framework. The core principle behind PINNs involves embedding well-established differential equations—representing physical laws—into the network's training process.

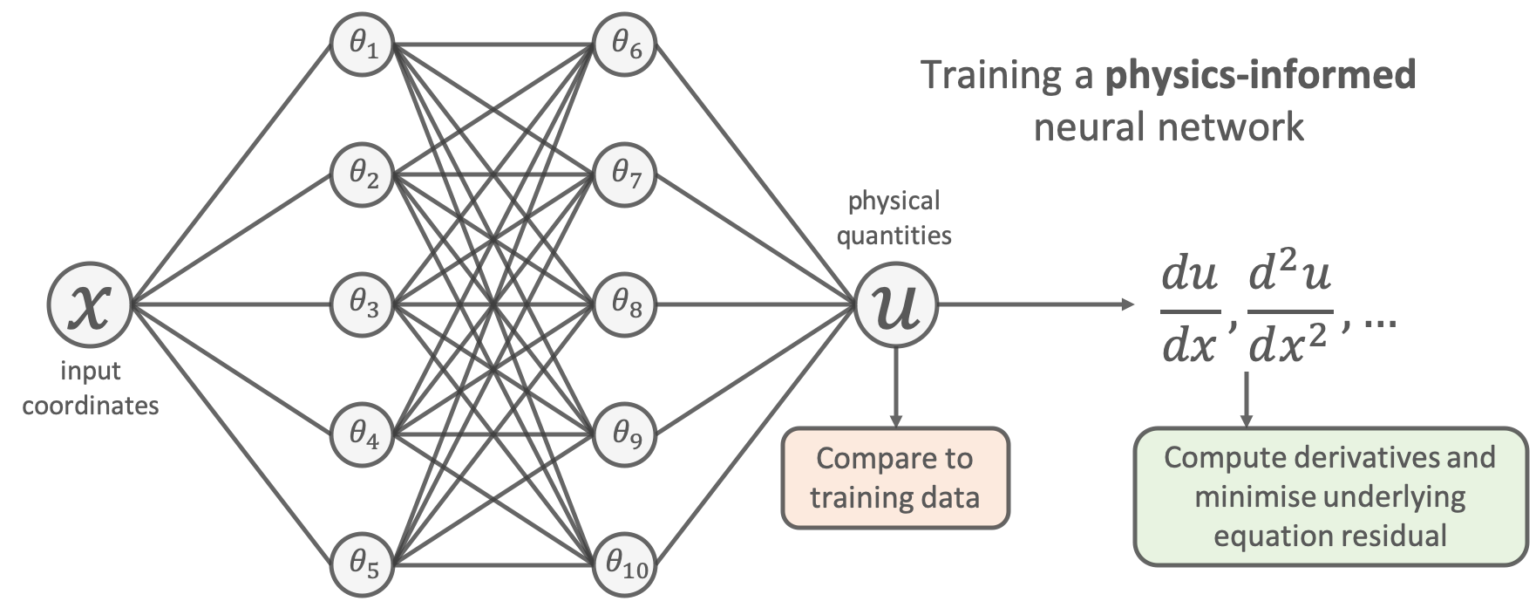
Schematic of physics-informed neural network (Source)

Here's how it works: The network is fed a set of input points. As it processes these points, it doesn't just aim to fit the training data; it also calculates its outputs' gradients concerning the inputs. These gradients are then used to compute the residuals of the physical equations at the input points. This residual computation, indicative of how well the network's outputs comply with the physical laws, is then incorporated into the network's loss function as an additional term.

Effectively, the loss function of a PINN has two main components: one that measures the discrepancy between the network's predictions and the actual data, and another that quantifies the deviation of the network's predictions from the physical model described by the differential equations. By minimizing this composite loss function, the network learns to predict outcomes that are not only consistent with the observed data but also aligned with the underlying physical principles.

This dual-objective optimisation ensures that the PINN's predictions are physically plausible across a broader range of scenarios, beyond the specific instances represented in the training data. Thus, PINNs offer a powerful approach for modeling complex systems where adherence to physical laws is as crucial as fitting the observed data.

Advantages Over Traditional Approaches

By combining data-driven learning with physical principles, PINNs offer several advantages:

  • Enhanced Predictive Power: They can make accurate predictions even in regions with sparse or no data, as they leverage the governing physical laws to guide the learning process.
  • Generalisation: PINNs are not confined to the data they are trained on; they can extrapolate and make reliable predictions under different conditions, thanks to their physics-informed foundation.
  • Reduced Data Dependence: Because they utilise known physics, PINNs can achieve high accuracy with less data, an invaluable trait in scenarios where data collection is challenging or expensive.

Tackling Complex Problems with PINNs

The methodology behind PINNs is not just a theoretical construct but has practical implications across various domains. For example, Ben Moseley's work on solving the wave equation with physics-informed deep learning showcases the capability of PINNs to address complex differential equations that are foundational in understanding a plethora of physical and engineering problems.

Some Key Characteristics of PINNs

PINNs are distinguished by several defining features:

  1. Integration of Physical Equations: They embed known physical laws into the neural network's architecture, ensuring that the model's predictions adhere to fundamental principles.
  2. Solving PDEs: PINNs are adept at solving partial differential equations (PDEs), which describe the behaviour of various physical systems.
  3. Data Efficiency: They require fewer data points for training, thanks to their ability to leverage both data and encoded physical knowledge.
  4. Hybrid Learning: This approach combines supervised learning with physical constraints, enhancing the model's generalisation capabilities.
  5. Mesh-Free Approach: PINNs do not depend on predefined meshes, allowing them to handle complex geometries more flexibly.
  6. Multi-fidelity Learning: They can incorporate information from multiple sources, enhancing the model's accuracy and robustness.
  7. Regularisation through Physics: Physical constraints serve as regularisation terms, guiding the network toward realistic solutions.
  8. Inverse Problem Solving: PINNs excel at inferring parameters or conditions from observed data, broadening their applicability across various fields.

Training and Implementation

Training a PINN involves a hybrid loss function that includes both data-driven terms and physics-based constraints. For instance, in modelling fluid flow, the loss function would incorporate terms that ensure mass conservation. The network learns to align its predictions with both the available data and the physical laws, enabling it to model physical systems with remarkable accuracy.

PINNs for Fluid Mechanics

Future Directions and Challenges

While PINNs represent a significant leap forward, the journey is far from complete. The field continues to evolve, with ongoing research aimed at enhancing the efficiency, scalability, and applicability of PINNs to a broader array of problems. Challenges such as dealing with highly nonlinear systems, optimizing training strategies, and integrating disparate sources of physical knowledge remain at the forefront of this exciting intersection of machine learning and physics.

Other Resources

Check out this page: (https://maziarraissi.github.io/PINNs/)

Conclusion

Physics-informed neural Networks (PINNs) are transforming the landscape of deep learning by integrating the rigor of physical laws into neural network architectures. This synergy between domain-specific knowledge and advanced machine-learning techniques opens new horizons for research and application, making PINNs a cornerstone in the evolution of intelligent systems.

As we advance in our exploration of AI, the confluence of physics-based knowledge and neural networks heralds a promising future, paving the way for more accurate, reliable, and insightful predictive models.

If you would love to see other articles, please check them out by clicking the button below!👇

Read More

Keep engineering your mind!

Jousef