Introduction 📖

The goal is to separate a given differential equation of n-th order in n differential equations of first order. The following ODE for a single mass oscillator with damping d, external excitation F und spring stiffness c is given:

\[ m\ddot{y} + d\dot{y} + cy = F \]

Code 👨‍💻

ode45.m - Script

% MATLAB - Solving an ODE (Ordinary Differential Equation)
% November, 17th 2019
% Jousef Murad - www.jousefmurad.com
% MATLAB Version - R2019b

clc, clear, close all

%% Single-degree-of-freedom oscillator

% ==========
% Parameter Definition
% ==========

m = 1;
c = 1;
d = 100;
f = 0;

% ==========
% Initial and Boundary Conditions 
% ==========

Time = 0:0.1:40; % 1x2 Matrix

IC = [0; 0.01]; % 2x1 Matrix

% ==========
% Solver Options
% ==========

SolverOptions = odeset('RelTol',1e-5,'AbsTol',1e-5);

% ODE45 Solver

[T,Y] = ode45(@StateSpaceForm,Time, IC, SolverOptions, m, d, c, f);

% ==========
% Plotting
% ==========

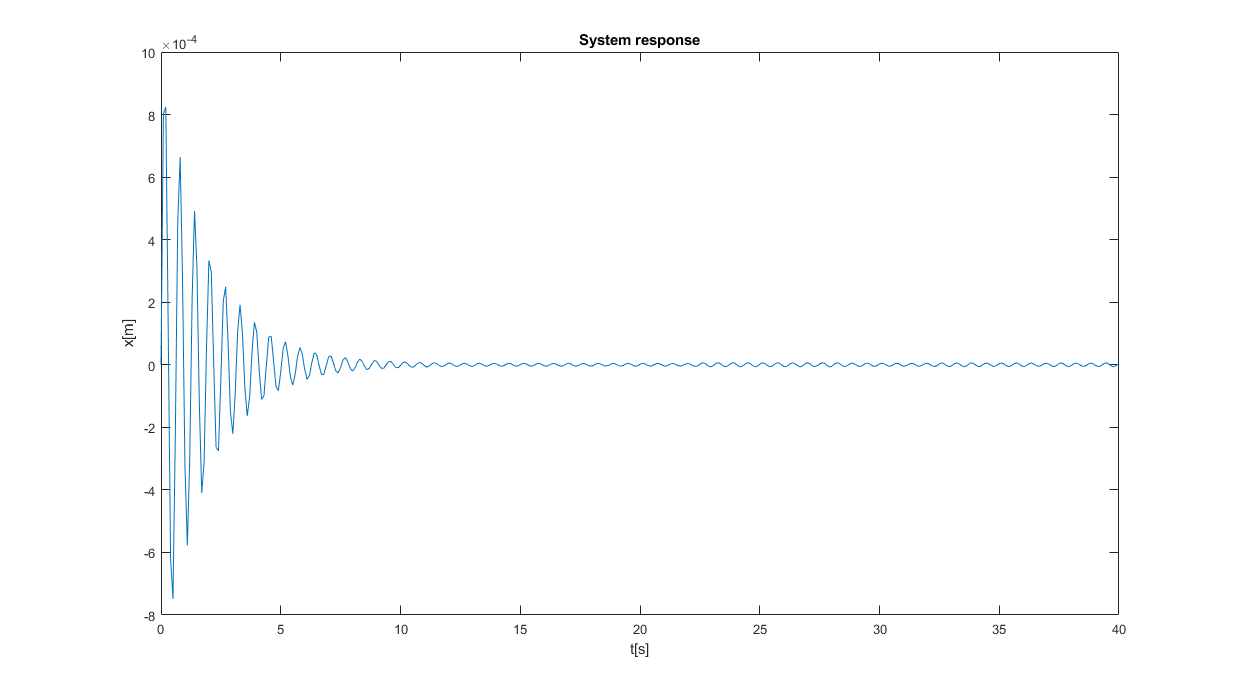
%plot(T,Y(:,1),'b',T,Y(:,2),'r');

fig1 = figure(1);
movegui(fig1,'northeast');
plot(T,Y(:,1));
title('System response');
xlabel('t[s]');
ylabel('x[m]');


% ==========
% Multiple Plots
% ==========

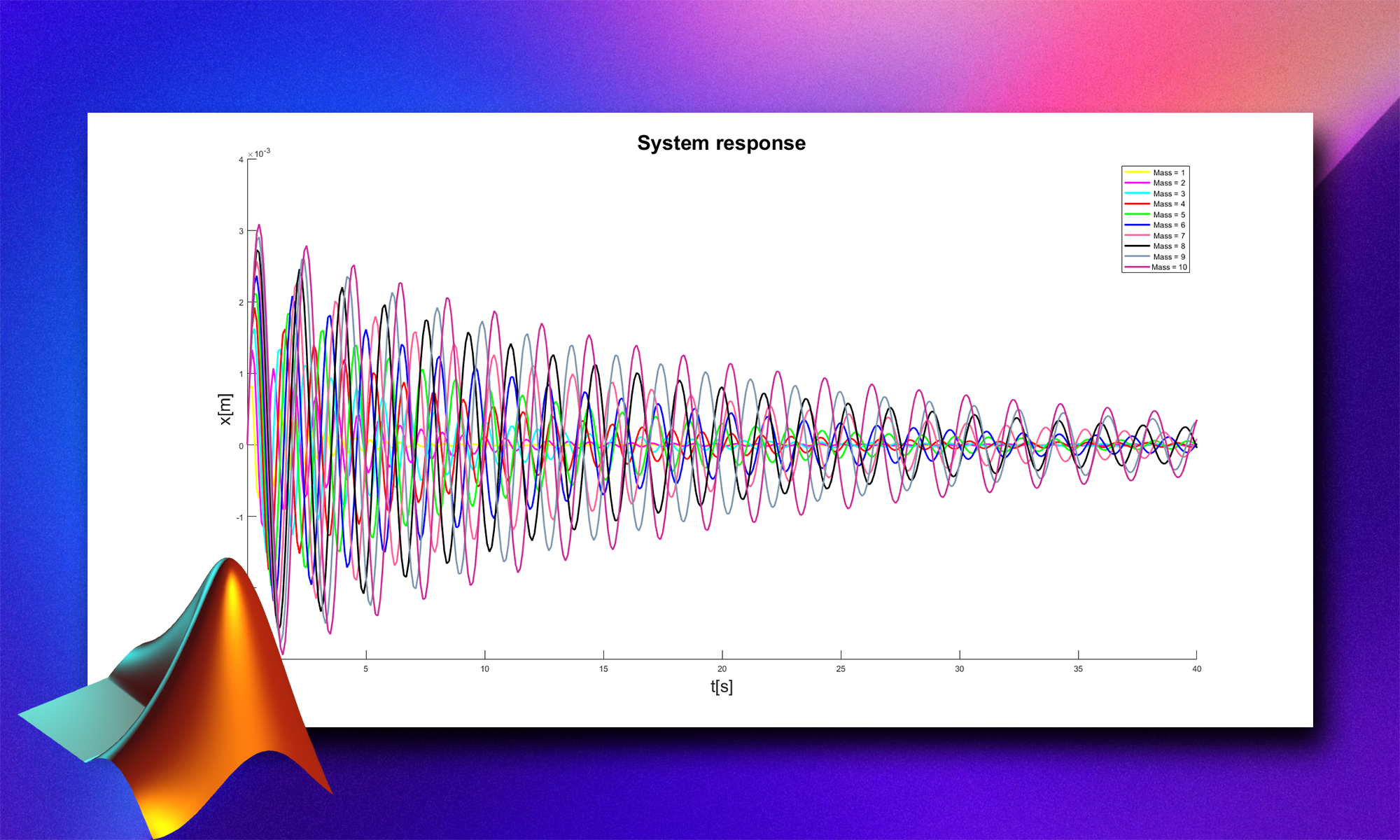
fig2 = figure(2);

for m = 1:1:10
    
    [T,Y] = ode45(@StateSpaceForm,Time, IC, SolverOptions, m, d, c, f);
    
    Matrix(m,:) = [m Y(:,1)'];
    
    C = {'y','m','c','r','g','b',[1 0.4 0.6],'k',[.5 .6 .7],[.8 .2 .6]}; % Colors for plots
    
    hold on
    
    Plot1(m)= plot(T,Matrix(m,2:end),'LineWidth',2,'color',C{m});
    
    lgd=num2str([1:1:10]','Mass = %d');

    h = legend(Plot1,lgd);
    
    %set(h,'FontSize',12); 
    
    title('System response','FontSize', 24);
    
    xlabel('t[s]','FontSize', 20);
    
    ylabel('x[m]','FontSize', 20);
   
    
end

movegui(fig2,'southeast');

State Space Form - Function

function [ xp ] = StateSpaceForm( t,x,m,c,d,f )
% State space form for single mass oscillator
xp=[x(2); (1/m)*(f-d*x(2)-c*x(1))];

end

The code for multiple plots and for solving the ODE can be found in my Github repo.

PDF Download 🌏👨‍💻

Download the complete instruction to derive the state space representation and implementation to MATLAB below👇

If that post was helpful to you, consider subscribing to my latest blogs, tutorials and course updates – costs you less than a Starbucks coffee! 😉

Keep engineering your mind! ❤️

Jousef