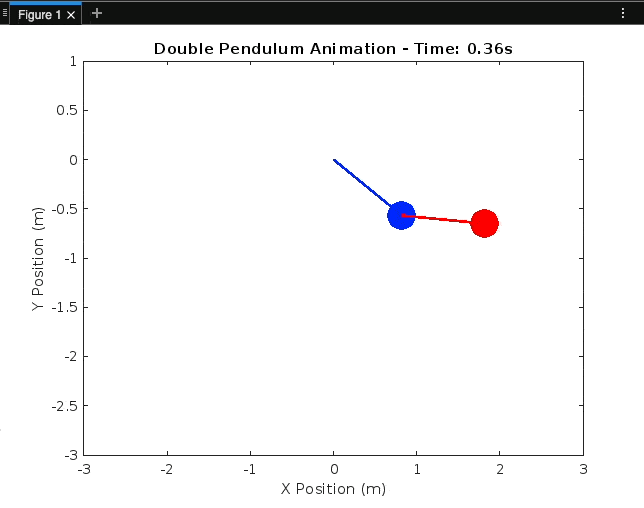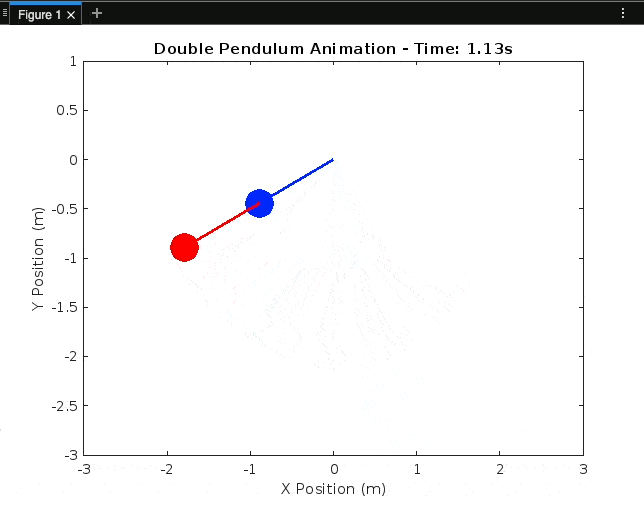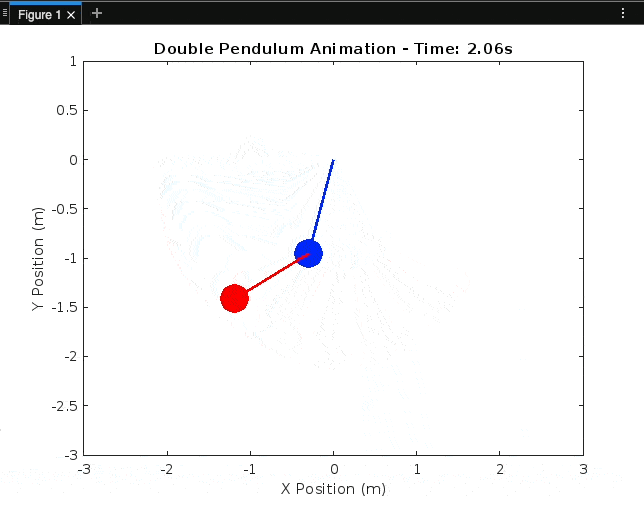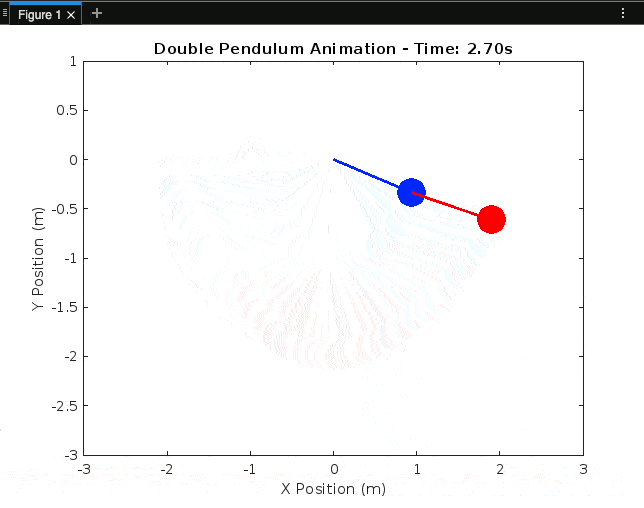
In this blog post, part 2 of the Double Pendulum blog series, we'll explore the fascinating world of double pendulums and demonstrate how to simulate their motion using MATLAB. Double pendulums are a classic example of a chaotic system, and their behaviour can be mesmerising to watch. We'll walk through the code step by step, explaining each part.
Understanding the Double Pendulum
A double pendulum consists of two arms connected end-to-end, with the second pendulum hanging from the first. This system is a classic example of chaotic behaviour, where small changes in initial conditions can lead to dramatically different outcomes.
A set of coupled nonlinear differential equations describes the motion of a double pendulum. To simulate its motion, we'll use numerical integration methods provided by MATLAB.
Setting Up the Environment
Let's start by setting up our MATLAB environment:
% Double Pendulum Simulation
clear;
close all;- clear - clears the workspace to start with a clean slate.
- close all - closes any open figures to ensure a fresh start for plotting.
Defining Parameters
Next, we define the physical parameters of the double pendulum:
% Define Parameters
g = 9.81; % Acceleration due to gravity (m/s^2)
L1 = 1.0; % Length of the first pendulum arm (m)
L2 = 1.0; % Length of the second pendulum arm (m)
m1 = 1.0; % Mass of the first pendulum bob (kg)
m2 = 1.0; % Mass of the second pendulum bob (kg)- g = 9.81 - sets the acceleration due to gravity, a fundamental parameter for the pendulum's behaviour.
- L1 = 1.0 and L2 = 1.0 - define the lengths of the two pendulum arms.
- m1 = 1.0 and m2 = 1.0 - Specify the masses of the pendulum bobs.
Initial Conditions
We need to set the initial conditions for the simulation:
% Initial conditions
theta1_0 = pi / 2; % Initial angle of the first pendulum (radians)
theta2_0 = pi / 2; % Initial angle of the second pendulum (radians)
omega1_0 = 0; % Initial angular velocity of the first pendulum (rad/s)
omega2_0 = 0; % Initial angular velocity of the second pendulum (rad/s)- theta1_0 and theta2_0 are the initial angles of the first and second pendulum bobs.
- omega1_0 and omega2_0 are the initial angular velocities of the bobs.
Time Settings
We set up the time parameters for the simulation:
% Time settings
tspan = [0 5]; % Time span for simulation (seconds)
dt = 0.001; % Time step (seconds)- tspan = [0 20] defines the time span for the simulation, starting from 0 seconds and ending at 20 seconds.
- dt = 0.01 specifies the time step used for numerical integration. Smaller time steps provide more accurate results but may require more computation.
Numerical Integration with ODE45
We'll use the ODE45 solver for numerical integration. The equations of motion are defined in the doublePendulumODE function:
% Numerical integration using ODE45
options = odeset('RelTol', 1e-6, 'AbsTol', 1e-6);
[t, y] = ode45(@(t, y) doublePendulumODE(t, y, g, L1, L2, m1, m2), tspan, [theta1_0, omega1_0, theta2_0, omega2_0], options);- [t, y] = ode45(...) calls the ODE45 solver to numerically integrate the system of ordinary differential equations (ODEs) defined by the function
doublePendulumODE. The solver returns time values in t and the solution to the ODEs in y. - @(t, y) doublePendulumODE(t, y, g, L1, L2, m1, m2) provides the ODE solver with the ODE function
doublePendulumODEand the necessary input parameters, including time t, state vector y, and the system parameters (g, L1, L2, m1, and m2).
odeset is used to set options for the ODE45 solver, which is a function in MATLAB used for solving ordinary differential equations (ODEs) numerically.
Here's an explanation of the line:
options: This variable is assigned the output of theodesetfunction, which is used to create a structure specifying various options for the ODE solver.'RelTol', 1e-6: This sets the relative tolerance for the solver. Relative tolerance is a measure of how accurately the solver should control the relative error in the solution. In this case, it's set to1e-6, which is a shorthand notation for 1×10^−6.'AbsTol', 1e-6: This sets the absolute tolerance for the solver. Absolute tolerance is a measure of the absolute error in the solution. Similar to relative tolerance, it's set to1e-6.
Extracting and Converting Data
We extract and convert the data to x, y positions:
% Extract angles
theta1 = y(:, 1);
theta2 = y(:, 3);
% Convert angles to x, y positions of pendulum bobs
x1 = L1 * sin(theta1);
y1 = -L1 * cos(theta1);
x2 = x1 + L2 * sin(theta2);
y2 = y1 - L2 * cos(theta2);- theta1 and theta2 - extract the angles of the first and second pendulum bobs from the solution y.
- x1, y1, x2, and y2 - calculate the x and y positions
Animation Setup
We create a plot to visualise the motion of the double pendulum:
% Animation
% Initialize an array to store frames for the animation
frames = [];
% Create a figure for the animation
animationFig = figure;
% Set manual axes limits for animation
animationLimits = [-3 3 -3 1]; % Adjust as needed
% Set initial axes limits
axis(animationLimits);- frames = [] - initialise an empty array to store frames for the animation.
- animationFig = figure - creates a figure for the animation.
- animationLimits = [-3 3 -3 1] - sets manual axes limits for the animation. These limits determine the visible portion of the animation.
- axis(animationLimits) - sets the initial axes limits of the animation figure.
Animation Loop
for i = 1:length(t)
% Update the position of the pendulum bobs and rods in the animation plot
plot([0, x1(i)], [0, y1(i)], 'b', 'LineWidth', 2); % Rod for Pendulum 1
hold on;
plot(x1(i), y1(i), 'bo', 'MarkerSize', 20, 'MarkerFaceColor', 'b'); % Mass for Pendulum 1
plot([x1(i), x2(i)], [y1(i), y2(i)], 'r', 'LineWidth', 2); % Rod for Pendulum 2
plot(x2(i), y2(i), 'ro', 'MarkerSize', 20, 'MarkerFaceColor', 'r'); % Mass for Pendulum 2
xlabel('X Position (m)');
ylabel('Y Position (m)');
title(['Double Pendulum Animation - Time: ', num2str(t(i), '%.2f'), 's']);
% Set initial y-axis limits
ylim(animationLimits(3:4));
xlim(animationLimits(1:2));
% Capture the current frame for the animation
frame = getframe(animationFig);
frames = [frames, frame];
% Clear the previous frame in the animation plot
if i < length(t)
cla(animationFig);
end
end
In this extended code:
- The loop iterates through each time step t(i) of the simulation.
- Pendulum positions and rods are updated in the animation plot using plot commands.
- xlabel, ylabel, and title are used to label the animation plot.
- ylim(animationLimits(3:4)) and xlim(animationLimits(1:2)) ensure that the y-axis limits remain constant during animation.
- getframe(animationFig) captures the current frame for the animation.
- cla(animationFig) clears the previous frame in the plot, preparing it for the next frame.
Animation Display
% Close the animation figure
close(animationFig);
% Display the animation
figure;
movie(frames, 1, 30); % Play the animation at 30 frames per second- close(animationFig) closes the animation figure.
- figure creates a new figure for displaying the animation.
- movie(frames, 1, 30) plays the animation using the frames captured during the simulation. The animation plays at 30 frames per second.
Double Pendulum ODE Function
% Define the function for the double pendulum ODEs
function dydt = doublePendulumODE(t, y, g, L1, L2, m1, m2)
% Unpack the state variables
theta1 = y(1);
omega1 = y(2);
theta2 = y(3);
omega2 = y(4);
% Equations of motion for the double pendulum
dydt = zeros(4, 1);
dydt(1) = omega1;
dydt(2) = (-g * (2 * m1 + m2) * sin(theta1) - m2 * g * sin(theta1 - 2 * theta2) - 2 * sin(theta1 - theta2) * m2 * (omega2^2 * L2 + omega1^2 * L1 * cos(theta1 - theta2))) / (L1 * (2 * m1 + m2 - m2 * cos(2 * theta1 - 2 * theta2)));
dydt(3) = omega2;
dydt(4) = (2 * sin(theta1 - theta2) * (omega1^2 * L1 * (m1 + m2) + g * (m1 + m2) * cos(theta1) + omega2^2 * L2 * m2 * cos(theta1 - theta2))) / (L2 * (2 * m1 + m2 - m2 * cos(2 * theta1 - 2 * theta2)));
endFunction Signature
function dydt = doublePendulumODE(t, y, g, L1, L2, m1, m2)- t is the current time.
- y is the state vector containing the angles and angular velocities of the double pendulum.
- g, L1, L2, m1, m2: Parameters representing gravity, lengths, and masses of the pendulum components.
Unpacking State Variables:
theta1 = y(1);
omega1 = y(2);
theta2 = y(3);
omega2 = y(4);- theta1, omega1, theta2, and omega2 are unpacked from the state vector y. They represent the angles and angular velocities of the two pendulum components.
Equations of Motion
dydt = zeros(4, 1);
dydt(1) = omega1;
dydt(2) = (-g * (2 * m1 + m2) * sin(theta1) - m2 * g * sin(theta1 - 2 * theta2) - 2 * sin(theta1 - theta2) * m2 * (omega2^2 * L2 + omega1^2 * L1 * cos(theta1 - theta2))) / (L1 * (2 * m1 + m2 - m2 * cos(2 * theta1 - 2 * theta2)));
dydt(3) = omega2;
dydt(4) = (2 * sin(theta1 - theta2) * (omega1^2 * L1 * (m1 + m2) + g * (m1 + m2) * cos(theta1) + omega2^2 * L2 * m2 * cos(theta1 - theta2))) / (L2 * (2 * m1 + m2 - m2 * cos(2 * theta1 - 2 * theta2)));- dydt is the output vector representing the derivatives of the state variables with respect to time.
- The equations of motion describe how the angles and angular velocities change over time for the double pendulum system.
- These equations are derived from the Lagrangian formulation for the double pendulum system.
This function is used in the ODE solver (ode45) to numerically integrate the system of ordinary differential equations, allowing simulation of the double pendulum's motion over time.
Full Code
% Double Pendulum Simulation
% Clear workspace and close any open figures
clear;
close all;
clc;
% Define Parameters
g = 9.81; % Acceleration due to gravity (m/s^2)
L1 = 1.0; % Length of the first pendulum arm (m)
L2 = 1.0; % Length of the second pendulum arm (m)
m1 = 1.0; % Mass of the first pendulum bob (kg)
m2 = 1.0; % Mass of the second pendulum bob (kg)
% Initial Conditions
theta1_0 = pi / 2; % Initial angle of the first pendulum (radians)
theta2_0 = pi / 2; % Initial angle of the second pendulum (radians)
omega1_0 = 0; % Initial angular velocity of the first pendulum (rad/s)
omega2_0 = 0; % Initial angular velocity of the second pendulum (rad/s)
% Time Settings
tspan = [0 10]; % Extend the time span for simulation (seconds)
dt = 0.001; % Reduce the time step (seconds)
% Numerical Integration using ODE45
options = odeset('RelTol', 1e-6, 'AbsTol', 1e-6);
[t, y] = ode45(@(t, y) doublePendulumODE(t, y, g, L1, L2, m1, m2), tspan, [theta1_0, omega1_0, theta2_0, omega2_0], options);
% Extracting and Converting Data
theta1 = y(:, 1);
theta2 = y(:, 3);
x1 = L1 * sin(theta1);
y1 = -L1 * cos(theta1);
x2 = x1 + L2 * sin(theta2);
y2 = y1 - L2 * cos(theta2);
% Animation
% Initialize an array to store frames for the animation
frames = [];
% Create a figure for the animation
animationFig = figure;
% Set manual axes limits for animation
animationLimits = [-3 3 -3 1]; % Adjust as needed
% Set initial axes limits
axis(animationLimits);
for i = 1:length(t)
% Update the position of the pendulum bobs and rods in the animation plot
plot([0, x1(i)], [0, y1(i)], 'b', 'LineWidth', 2); % Rod for Pendulum 1
hold on;
plot(x1(i), y1(i), 'bo', 'MarkerSize', 20, 'MarkerFaceColor', 'b'); % Mass for Pendulum 1
plot([x1(i), x2(i)], [y1(i), y2(i)], 'r', 'LineWidth', 2); % Rod for Pendulum 2
plot(x2(i), y2(i), 'ro', 'MarkerSize', 20, 'MarkerFaceColor', 'r'); % Mass for Pendulum 2
xlabel('X Position (m)');
ylabel('Y Position (m)');
title(['Double Pendulum Animation - Time: ', num2str(t(i), '%.2f'), 's']);
% Set initial y-axis limits
ylim(animationLimits(3:4));
xlim(animationLimits(1:2));
% Capture the current frame for the animation
frame = getframe(animationFig);
frames = [frames, frame];
% Clear the previous frame in the animation plot
if i < length(t)
cla(animationFig);
end
end
% Close the animation figure
close(animationFig);
% Display the animation
figure;
movie(frames, 1, 30); % Play the animation at 30 frames per second
% Define the function for the double pendulum ODEs
function dydt = doublePendulumODE(t, y, g, L1, L2, m1, m2)
% Unpack the state variables
theta1 = y(1);
omega1 = y(2);
theta2 = y(3);
omega2 = y(4);
% Equations of motion for the double pendulum
dydt = zeros(4, 1);
dydt(1) = omega1;
dydt(2) = (-g * (2 * m1 + m2) * sin(theta1) - m2 * g * sin(theta1 - 2 * theta2) - 2 * sin(theta1 - theta2) * m2 * (omega2^2 * L2 + omega1^2 * L1 * cos(theta1 - theta2))) / (L1 * (2 * m1 + m2 - m2 * cos(2 * theta1 - 2 * theta2)));
dydt(3) = omega2;
dydt(4) = (2 * sin(theta1 - theta2) * (omega1^2 * L1 * (m1 + m2) + g * (m1 + m2) * cos(theta1) + omega2^2 * L2 * m2 * cos(theta1 - theta2))) / (L2 * (2 * m1 + m2 - m2 * cos(2 * theta1 - 2 * theta2)));
end
Conclusion
In this blog post, we've explored the mesmerising world of double pendulums and learned how to simulate their complex and chaotic motion using MATLAB. The provided code offers a simplified introduction to the topic, and there are endless opportunities for further exploration and visualisation, which we might tackle in the third and last part of this introductory series.
Double pendulums are a great example of how seemingly simple systems can exhibit rich and unpredictable behaviours. Exploring their motion and simulating it in MATLAB can be a rewarding and educational experience.
If this post was helpful to you, consider subscribing to receive the latest updates! 🙂
And if you would love to see other blog posts or tutorials on MATLAB, comment under this post - cheers!
Keep engineering your mind! ❤️
Jousef

